Materi Segitiga Lengkap dengan Contoh Soal dan Pembahasannya ~ Haloo adik-adik, selamat datang di Agus Blog. Blog pendidikan tempat berbagi dan belajar.

Pada kesempatan kali ini Agus Blog akan membahas materi kelas 7 SMP yaitu bab Segitiga, berikut penjelasan selengkapnya :

Pengertian Segitiga

Apa itu segitiga ?

Segitiga atau segi tiga (bahasa Inggris: triangle) adalah nama suatu bentuk yang dibuat dari tiga sisi yang berupa garis lurus dan tiga sudut

Jenis Jenis Segitiga

1. Jenis segitiga berdasarkan panjang sisinya

Berdasarkan panjang sisinya, segitiga dibagi menjadi 3 jenis yaitu :

Segitiga sama sisi

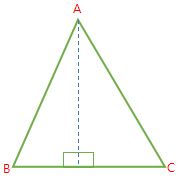
Segitiga sama kaki adalah segitiga yang ketiga sisinya sama panjang.

AB = BC = AC

Segitiga sama kaki

Segitiga sama sisi adalah segitiga yang dua dari 3 sisinya itu sama panjang.

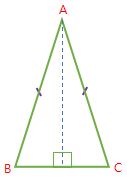
AB = AC

Segitiga sembarang

Segitiga semabarang adalah segitiga yang tidak memiliki sisi yang sama panjang.

2. Jenis Segitiga Berdasarkan Sudut-sudutnya

Segitiga Lancip

Segitiga lancip adalah segitiga yang ketiga sudutnya kurang dari 90o.

Segitiga Tumpul

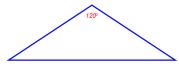
Segitiga Tumpul adalah segitiga yang salah satu sudutnya lebih dari 90o.

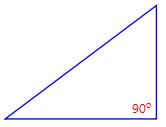
Segitiga Siku-siku

Segitiga Siku-siku adalah segitiga yang salah satu sudutnya sama dengan 90o.

Jumlah Sudut – Sudut pada Segitiga

Untuk mengetahui jumlah sudut segitiga, Buatlah sembarang segitiga ABC dengan ketiga sudut yang tidak perlu hitung terlebih dahulu. Nantinya, akan dibuktikan melalui percobaan sederhana bahwa jumlah sudut – sudut pada segitiga tersebut adalah 180o.

Potong masing – masing sudut sehingga didapat tiga buah potongan sudut segitiga tersebut. Potongan tiga sudut segitiga kemudian gabungkan menjadi satu. Gabungan ketiga sudut segitiga tersebut akan membentuk sebuah garis lurus. Sehingga, dapat diambil kesimpulan bahwa jumlah sudut – sudut pada segitiga sama adalah 180o. Itulah asal angka 180o yang mewakili jumlah sudut – sudut pada segitiga.

Teorema Ketaksamaan Segitiga

pada segitiga, teorema ini berbunyi bahwa jumlah dari panjang dua sisi pada segitiga selalu lebih besar dari panjang sisi satunya.

untuk lebih jelas tentang penerapan teorema ini silahkan lihat contoh berikut :

Contoh soal 1

Jika diketahui tiga buah bilangan bulat positif 4, 5, 6. Tentukan apakah tiga bilangan ini dapat menjadi sebuah sisi segitiga.

jawab:

diketahui: a = 4, b = 5 dan c = 6.

4 < 5 + 6 (benar)

5 < 4 + 6 (benar)

6 < 4 + 5 (benar)

4 > |5 - 6| (benar)

5 > |4 - 6| (benar)

6 > |4 - 5| (benar)

Karena semua pengecekan berdasarkan ketidaksamaan segitiga benar maka 4, 5, 6 dapat menjadi sisi-sisi segitiga.

Contoh soal 2

Jika diketahui tiga buah bilangan bulat positif 5, 7, 12. Tentukan apakah tiga bilangan ini dapat menjadi sebuah sisi segitiga.

jawab:

diketahui: a = 5, b = 7 dan c = 12.

5 < 7 + 12 (benar)

7 < 5 + 12 (benar)

12 < 5 + 7 (salah)

5 > |7 - 12| (salah)

7 > |5 - 12| (salah)

12 > |5 - 7| (salah)

Karena tidak semua pengecekan berdasarkan ketidaksamaan segitiga benar maka 5, 7, 12 tidak dapat menjadi sisi-sisi segitiga.

Keliling Segitiga

Keliling segitiga dihitung dengan menjumlahkan panjang semua sisinya.

K = sisi 1 + sisi 2 + sisi 3

Luas Segitiga

Sedangkan luas segitiga merupakan setengah dari hasil kali alas dan tingginya. Dimana tinggi merupakan garis tegak lurus dari salah satu sisi ke titik sudut yang berseberangan.

L = ½ × alas × tinggi

Contoh Soal :

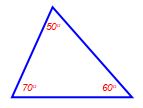
1. Mencari Salah Satu Sudut Segitiga

Berapakah besar sudut B pada gambar diatas

Dalam segitiga, jika ketiga sudutnya dijumlahkan akan selalu bernilai 180^o

∠A + ∠ B + ∠ C = 180^o

70 + ∠ B + 30 = 180^o

100 + ∠ B = 180

∠ B = 180 - 100

∠ B = 80^o

2. Soal Jumlah Sudut – Sudut pada Segitiga

Perhatikan gambar!

Besar sudut BAC adalah …. (Soal UN SMP 2019)

A. 24o

B. 28o

C. 55o

D. 65o

Pembahasan:

Jumlah sudut – sudut pada segitiga adalah 180o.

Menghitung nilai x:
$\angle A + \angle B + \angle C = 180^{o}$
$2x + 4^{o} + 4x + 7^{o} + 8x + 1^{o} = 180^{o}$
$2x + 4x + 8x + 4^{o} + 7^{o} + 1^{o} = 180^{o}$
$14x + 12^{o} = 180^{o}$
$14x = 180^{o} - 12^{o}$
$14x = 168^{o}$
$x = \frac{168^{o}}{14} = 12^{o}$

Menghitung sudut BAC:
$\angle BAC = \angle A$
$\angle BAC = 2x + 4^{o}$
$\angle BAC = 2 \times 12^{o} + 4^{o}$
$\angle BAC = 24^{o} + 4^{o} = 28^{o}$

3. Soal Luas dan Keliling Segitiga

Sebuah segitiga ABC memiliki panjang sisi masing-masing AB = 5cm, AC = 5cm, dan BC 6cm. Jika panjang garis tegak lurus dari titik sudut A ke sisi BC adalah 4cm, hitunglah luas dan keliling segitiga ABC

Penyelesaian

Diketahui :

Ditanya : luas dan keliling segitiga ABC =…?

Jawab :

L = ½ × alas × tinggi

L = ½ × BC × t

L = ½ × 6cm × 4cm

L = 12cm2

K = sisi 1 + sisi 2 + sisi 3

K = 5cm + 5cm + 6cm

K = 16cm

Jadi, segitiga ABC mempunyai luas 12cm2 dan keliling 16cm.

4. Soal Mencari Alas atau Tinggi Segitiga

Diketahui sebuah segitiga memiliki luas 16 cm² dan tinggi 8 cm. Tentukan alas segitiga!

Diketahui:

Luas = 16 cm², a = 8 cm

Ditanya:

Alas segitiga!

Jawab:

Alas = (2 × Luas) ÷ t

Alas = (2 x 16 cm²) ÷ 8 cm

Alas = 32 cm² ÷ 8 cm = 4 cm

Sehingga, alas segitiga yaitu 4 cm.

5. Soal Mencari Luas Segitiga Tumpul

Ada Sebuah segitiga tumpul yang memiliki panjang alasnya= 10 cm dan juga memiliki tinggi=4 cm. cari dan hitunglah luas segitiga tersebut !

Penyelesaian :

Diketahui :

a = 10 cm

t = 4 cm

Ditanya : luas = …?

Jawab :

L = ½ x a x t

L = ½ x 10 x 4

L = 20 cm2

Jadi, luas segitiga tumpul tersebut adalah = 20 cm2

Sumber : idschool.net, Wikipedia.org, rumus.co.id, falensiocc.blogspot.com

Kunjungi Juga :

Rangkuman, Soal dan Pembahasan Materi Sudut yang Terbentuk Jika Garis Sejajar Dipotong Oleh Sebuah Garis

Demikian artikel tentang "Materi Segitiga Lengkap dengan Contoh Soal dan Pembahasannya" Semoga bermanfaat.

Materi Segitiga Lengkap dengan Contoh Soal dan Pembahasannya

Pengertian Segitiga

Jenis Jenis Segitiga